6.2.2 Sets

A set is a collection of unique elements.

Syntactically, a set is specified as a comma-separated list of expressions delimited by braces. {0, 1, 2} is a set of 3 elements. The empty set is entered as {} and displayed as Ø.

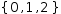
A set can be bound to a variable in a definition or associated with a variable in an equation following the same rules as binding tuples. When used in another expression, an explicit set variable can be entered using a type suffix s or ʂ^[1].

Sets interact with unary and binary operators and with scalars in the same way as tuples. There are also set-specific operators. Three of these – union, intersection and difference – take sets as operands and produce a set as a result. {a, b}∪{b, c} simplifies to {a, b, c}, {a, b}∩{b, c} simplifies to {b} and {a, b}⋅{b, c} simplifies to {a}. Another four operators take sets as operands and produce a Boolean result. 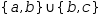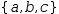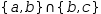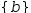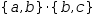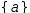They are subset (⊆) and proper subset (⊂) along with the negation of these ⊈ and ⊄. The final operator, ∈, tests for set containment. It takes an expression on the left and a set on the right.

The cardinality operator can be applied to sets, producing a real containing the element count.

The magnitude operator applied to sets works the same as for tuples, producing the sum of the squares of the elements.

The concatenation operator is not defined for sets. However, as it is defined for tuples, concatenation of two sets produces a tuple containing the two sets.

When tuples are used with set operators, they behave like multisets. When mixed with sets, tuples are constrained to sets before the set operator is applied.